Slope 2 is a fundamental concept in mathematics that plays a crucial role in various fields, including physics, engineering, and economics. Understanding slope and its applications is essential for students and professionals alike. In this article, we will delve into the intricacies of slope 2, its mathematical definition, and how it applies across different domains. We will also explore real-world examples and provide practical tips to better understand and utilize this concept.
Slope is essentially a measure of the steepness or incline of a line. It describes how much a line rises or falls as it moves horizontally. The concept of slope can be represented geometrically on a graph, where the slope is defined as the change in the vertical direction (rise) divided by the change in the horizontal direction (run). Slope 2 specifically refers to a particular case or example of slope that is often used in various mathematical contexts.
In this article, we will break down the concept of slope 2 into digestible sections, exploring its definition, calculation methods, applications in real-life scenarios, and much more. Whether you are a student looking to understand slope better or a professional seeking to apply it in your work, this comprehensive guide will provide valuable insights.
- Unveiling Maria Taylors Brother A Journey Through Family Ties And Shared Passions
- Unveiling The Mysteries Of The Predatorial Investigation Unit
Table of Contents
- Definition of Slope 2
- How to Calculate Slope 2
- Applications of Slope 2
- Real-World Examples of Slope 2
- Graphing Slope 2
- Common Mistakes in Calculating Slope 2
- Summary of Slope 2
- Additional Resources
Definition of Slope 2
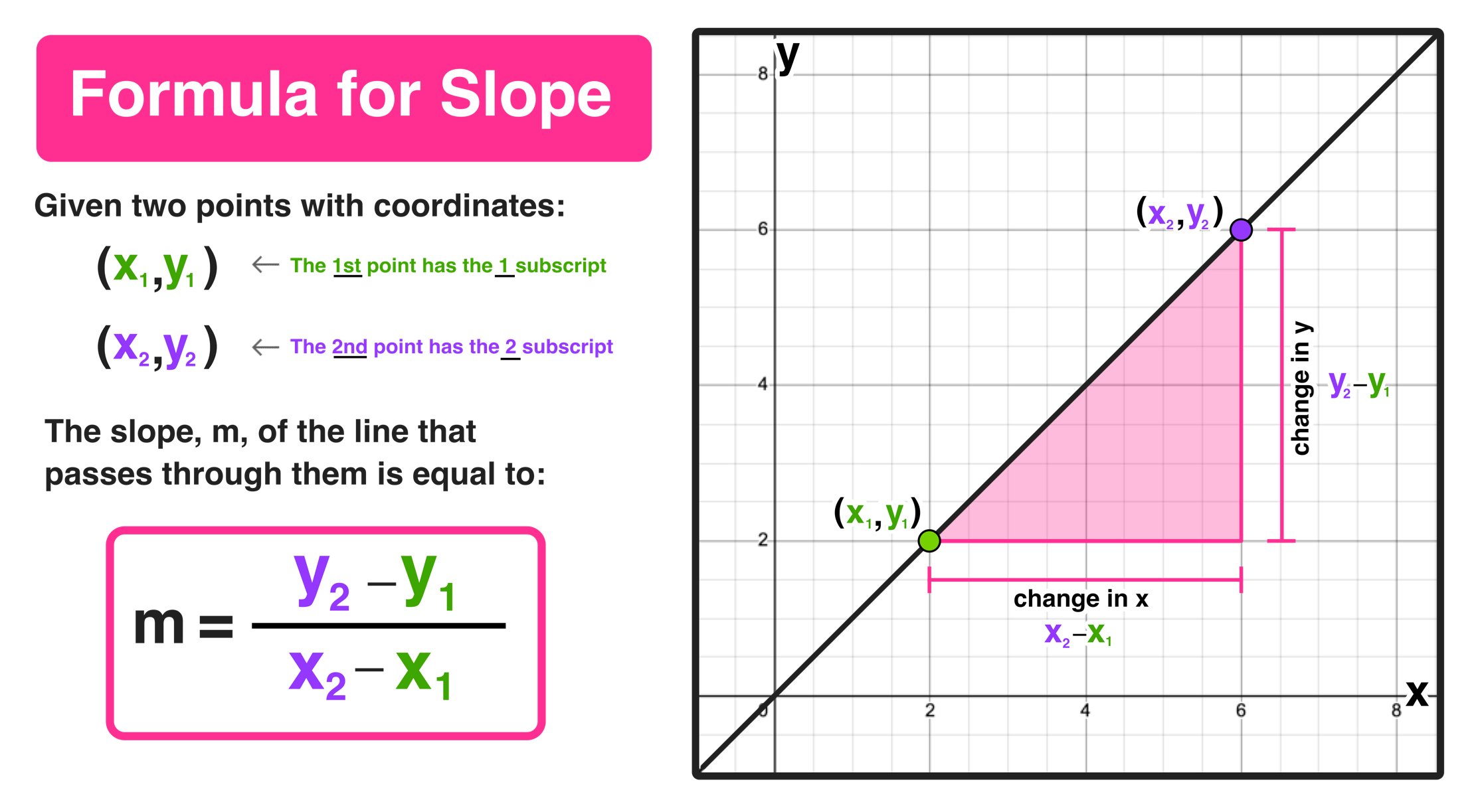
Slope 2 is defined as the ratio of the vertical change (rise) to the horizontal change (run) between two points on a line. Mathematically, it can be expressed as:
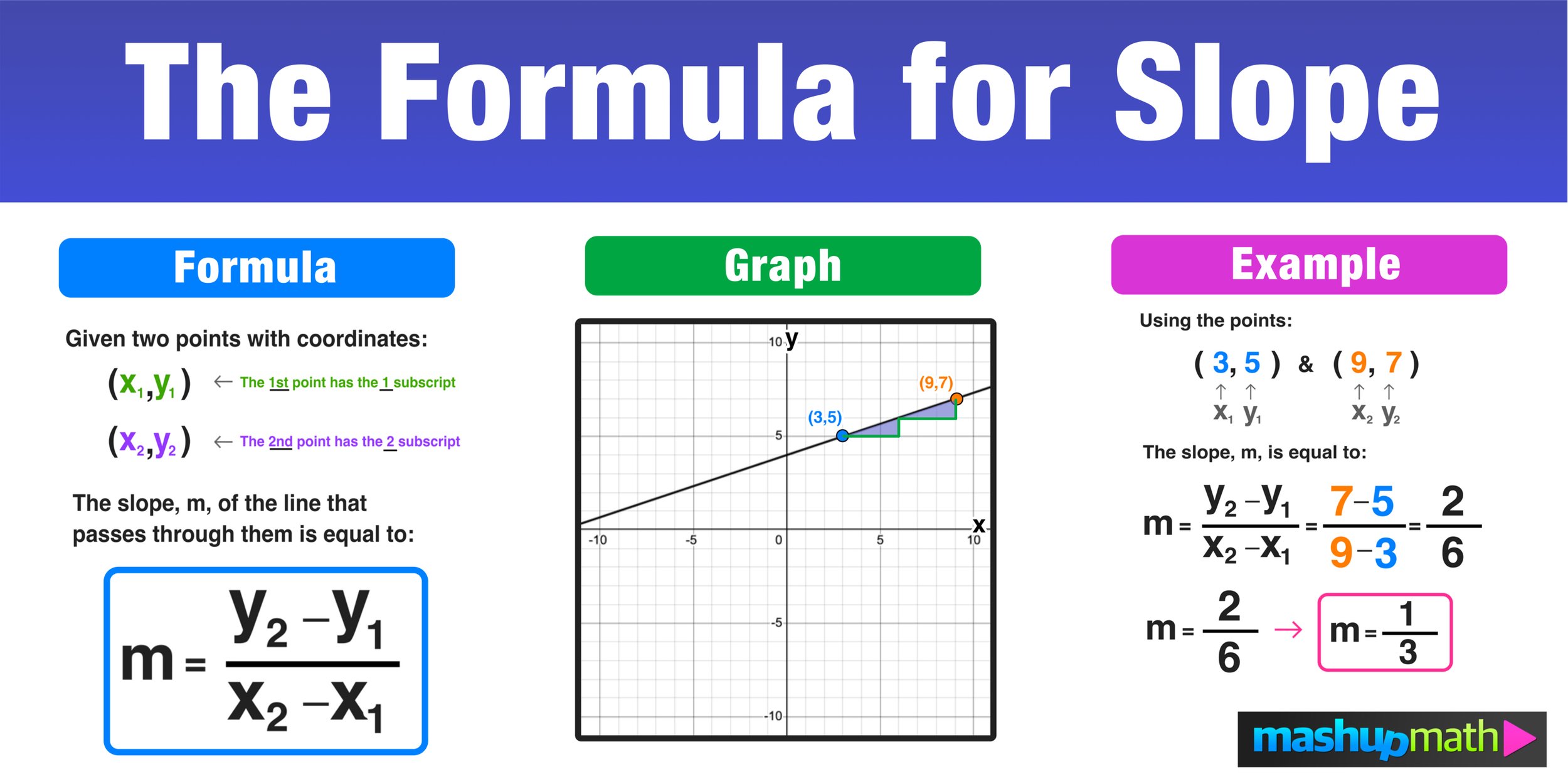
Slope (m) = (y2 - y1) / (x2 - x1)
Where (x1, y1) and (x2, y2) are two distinct points on the line. In many contexts, slope 2 is used to describe a particular case where the slope value is equal to 2, indicating that for every 1 unit of horizontal change, there is a 2 unit change in the vertical direction.
- Unveiling The Life Of Julie Jess A Comprehensive Insight
- Discovering The Allure Of Kirstentoosweet Onlyfan
How to Calculate Slope 2
Calculating slope 2 involves a few straightforward steps:
- Identify the two points (x1, y1) and (x2, y2) on the line.
- Subtract the y-values to find the rise (y2 - y1).
- Subtract the x-values to find the run (x2 - x1).
- Divide the rise by the run to find the slope.
For example, if we have two points (1, 3) and (3, 7), we can calculate the slope as follows:
Slope = (7 - 3) / (3 - 1) = 4 / 2 = 2
Applications of Slope 2
Slope 2 has various applications across different fields:
- Physics: In physics, the concept of slope is used to understand velocity and acceleration. For instance, a graph depicting distance vs. time will have a slope that represents speed.
- Economics: Economists use slope to determine the relationship between supply and demand. The slope of a demand curve can indicate how responsive consumers are to price changes.
- Engineering: In engineering, slope is used in the design of roads, ramps, and other structures to ensure safety and efficiency.
Real-World Examples of Slope 2
Let's explore some real-world scenarios where slope 2 is applicable:
Example 1: Construction
In construction, when designing a ramp for accessibility, a slope of 2 (or 2:1 ratio) might be used to ensure that it is not too steep for wheelchair users.
Example 2: Economics
A company may analyze its sales data, finding that a 2% increase in price results in a 4% decrease in quantity sold. This slope of -2 indicates the price elasticity of demand.
Graphing Slope 2
Graphing a line with a slope of 2 is simple. Starting from a point on the graph, you can move up 2 units and right 1 unit to mark the next point. This pattern continues, allowing you to draw a straight line that represents the slope visually.
Common Mistakes in Calculating Slope 2
When calculating slope, it's easy to make common mistakes:
- Confusing rise and run.
- Using the wrong coordinates for calculation.
- Forgetting to simplify the slope ratio.
Summary of Slope 2
In summary, slope 2 is a vital concept in mathematics with wide-ranging applications in various fields. Understanding how to calculate and interpret slope can enhance your analytical skills and provide insights into real-world scenarios. Remember to pay attention to detail when calculating slope to avoid common mistakes.
Additional Resources
For further reading, consider the following resources:
We hope this article has provided you with valuable insights into the concept of slope 2. If you have any questions or would like to share your thoughts, please leave a comment below. Don’t forget to share this article with others who may benefit from it, and check out our other articles for more informative content!
Thank you for reading, and we look forward to seeing you again for more engaging discussions and insights!